Brief review of social dilemmas in the framework of Game Theory
Today I want to briefly go over an introduction to the most common so-called social dilemmas in the framework of Game Theory. This will help you follow better my other post about Game Theory experiments.
Game Theory is a tool, frequently used by Mathematicians, Physicist, Sociologist, Economist and others, to model human behavior as it pertains to decision-making processes in different payoff scenarios. Typically, you have two individuals, two choices/actions available to them, and a corresponding payoff for each possible outcome. And you assume that, without talking to each other but knowing the rules, they make their independent decision.
As a well-known example, let's look at the The Prisoner's Dilemma game. It describes the following situation: you have two people in custody, in separated rooms, accused of the same crime. They have two options available to them, they can either cooperate (with the other person) and remain quiet, or they can defect (that is, accuse the other person). This gives four possible outcomes:
This framework actually describes a larger set of social dilemmas (more on this in a moment), but what makes it be The Prisoner's Dilemma game and not a different game, is the relative ordering of the four payoff parameters: T>R>P>S.
That is to say, in this game:
The classical equilibrium for this game is pure defection.
Now we are ready to describe the other common social dilemmas (remember that they all have the same matrix form, but the scenarios are different, so is the relative ordering of the four payoff parameters):
In the Snowdrift (or Chicken) game, you have the two individuals driving their cars in the same direction on a road that is blocked by the snow. Their options are again to cooperate or to defect, but now it means something else: cooperating means getting out of the car to manually plow the snow (so both drivers can get on their way), and defecting means staying in the car and doing nothing. In this game, the order of the payoffs for the four possible outcomes is: T > R > S > P. That is to say:
This is what is called an 'anti-coordination' game, because the best strategy is to do the opposite from what your opponent does (although remember that in this framework, both players make their decision independently and at the same time). The classical equilibrium for this game is a mixed one: one person cooperates, the other one defects.
Also, this game goes by another name: 'Chicken game', after the scene in the 1955 movie Rebel without a cause. In this situation, although the relative order of the payoff parameters is the same as in the Snowdrift, the stakes are somewhat higher: Two drivers race each other, towards a cliff. Cooperating in this case means to break before the road ends, while defecting means to drive on, no matter what. The winner is the driver that breaks last. You can see how this situation is essentially the same as the Snowdrift scenario from a Game Theory perspective, but the worst outcome is obviously worse: the driver doesn't break (D) and falls off, and so does the other driver (D), the best situation is when a driver. The second worst thing is to break first (C), while the other driver breaks second (D), and so on.
The Stag-Hunt game is a 'coordination game', and you'll see why. The situation is as follows: two hunters need to provide food for their families by going hunting. They can pick to go to a place where big buffaloes roam (C), or they could choose to go to a different part of the woods where rabbits live (D). We assume that they can't hunt a buffalo by themselves and need two people, but they can however hunt a rabbit alone. Also, it is better to share a buffalo that have one full rabbit. The four payoffs, sorted from best to worst are:
Or, in other words: R > T > P > S.
Finally, there is a rarely-used, rarely-studied game, where the relative payoff is R > S >P and R > T > P. That is to say, the most convenient action is to mutually cooperate. This is called the Harmony game, and you could argue that is kinda boring, because it presents to tension between what's best for the individual and what's best for the group.
It is customary to fixed the parameters P and R, leaving two free parameters, S and T. This way, you have a T-S plane, where the four quadrants correspond to the four social dilemmas described above.
As a summary, here they all are together, in a 2-D representation of the T-S plane:
Game Theory is a tool, frequently used by Mathematicians, Physicist, Sociologist, Economist and others, to model human behavior as it pertains to decision-making processes in different payoff scenarios. Typically, you have two individuals, two choices/actions available to them, and a corresponding payoff for each possible outcome. And you assume that, without talking to each other but knowing the rules, they make their independent decision.
As a well-known example, let's look at the The Prisoner's Dilemma game. It describes the following situation: you have two people in custody, in separated rooms, accused of the same crime. They have two options available to them, they can either cooperate (with the other person) and remain quiet, or they can defect (that is, accuse the other person). This gives four possible outcomes:
- individual #1 decides to cooperate (C) while individual #2 decides to defect (D) and betray her or him. We label the payoffs in this situation as S ('sucker's payoff') for individual #1, and T ('temptation to defect') for individual #2;
- you could have the reversed situation, where individual #1 defects and individual #2 cooperates. Here for individual #2 gets S and individual #2 gets T;
- you can have them both cooperate, both getting R (for 'reward');
- or both defect, both getting P ('punishment').
This framework actually describes a larger set of social dilemmas (more on this in a moment), but what makes it be The Prisoner's Dilemma game and not a different game, is the relative ordering of the four payoff parameters: T>R>P>S.
That is to say, in this game:
- the highest payoff corresponds to a defector that faces a cooperator (the defector gets to walk free, while the cooperator gets 10 years in jail);
- then the payoff for two cooperators (both get 1 year in jail, since the cops don't have enough evidence against them);
- next two defectors (similarly, now both would get 2 years in jail);
- worst-case scenario is when a cooperator faces a defector (as we already said in the fist situation, the cooperator gets 10 years in jail, while the defector gets to walk free, while).
The classical equilibrium for this game is pure defection.
Now we are ready to describe the other common social dilemmas (remember that they all have the same matrix form, but the scenarios are different, so is the relative ordering of the four payoff parameters):
In the Snowdrift (or Chicken) game, you have the two individuals driving their cars in the same direction on a road that is blocked by the snow. Their options are again to cooperate or to defect, but now it means something else: cooperating means getting out of the car to manually plow the snow (so both drivers can get on their way), and defecting means staying in the car and doing nothing. In this game, the order of the payoffs for the four possible outcomes is: T > R > S > P. That is to say:
- the best outcome is (again) for player #1 to stay in the car as the other driver plows the snow (player #1 does D, gets T);
- the second best option is if both drivers leave the car and plow the snow out (both play C, get R);
- next best option for player #1 is to dig out the snow while the other driver does nothing (player #1 does C, gets S);
- and clearly the worst option is when both drivers decide to do nothing (both do D, get P), since then nobody gets to go home.
This is what is called an 'anti-coordination' game, because the best strategy is to do the opposite from what your opponent does (although remember that in this framework, both players make their decision independently and at the same time). The classical equilibrium for this game is a mixed one: one person cooperates, the other one defects.
Also, this game goes by another name: 'Chicken game', after the scene in the 1955 movie Rebel without a cause. In this situation, although the relative order of the payoff parameters is the same as in the Snowdrift, the stakes are somewhat higher: Two drivers race each other, towards a cliff. Cooperating in this case means to break before the road ends, while defecting means to drive on, no matter what. The winner is the driver that breaks last. You can see how this situation is essentially the same as the Snowdrift scenario from a Game Theory perspective, but the worst outcome is obviously worse: the driver doesn't break (D) and falls off, and so does the other driver (D), the best situation is when a driver. The second worst thing is to break first (C), while the other driver breaks second (D), and so on.
The Stag-Hunt game is a 'coordination game', and you'll see why. The situation is as follows: two hunters need to provide food for their families by going hunting. They can pick to go to a place where big buffaloes roam (C), or they could choose to go to a different part of the woods where rabbits live (D). We assume that they can't hunt a buffalo by themselves and need two people, but they can however hunt a rabbit alone. Also, it is better to share a buffalo that have one full rabbit. The four payoffs, sorted from best to worst are:
- one hunter goes for the buffalo, and so does the other (both get R);
- second best situation, a hunter decides to go for the rabbit while the other tries for the buffalo while the other trying to go for the buffalo (player #1 does D, gets T).
- one hunter decides to go for the rabbit and so does the other (both play D, both get P);
- lastly, one hunter decides to go for the buffalo while the other goes for the rabbit (player #1 plays C, gets... nothing, really, S)
Or, in other words: R > T > P > S.
Finally, there is a rarely-used, rarely-studied game, where the relative payoff is R > S >P and R > T > P. That is to say, the most convenient action is to mutually cooperate. This is called the Harmony game, and you could argue that is kinda boring, because it presents to tension between what's best for the individual and what's best for the group.
It is customary to fixed the parameters P and R, leaving two free parameters, S and T. This way, you have a T-S plane, where the four quadrants correspond to the four social dilemmas described above.
As a summary, here they all are together, in a 2-D representation of the T-S plane:
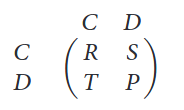


Comments